[백준] 타임머신 (11657번) - Python/Algorithm

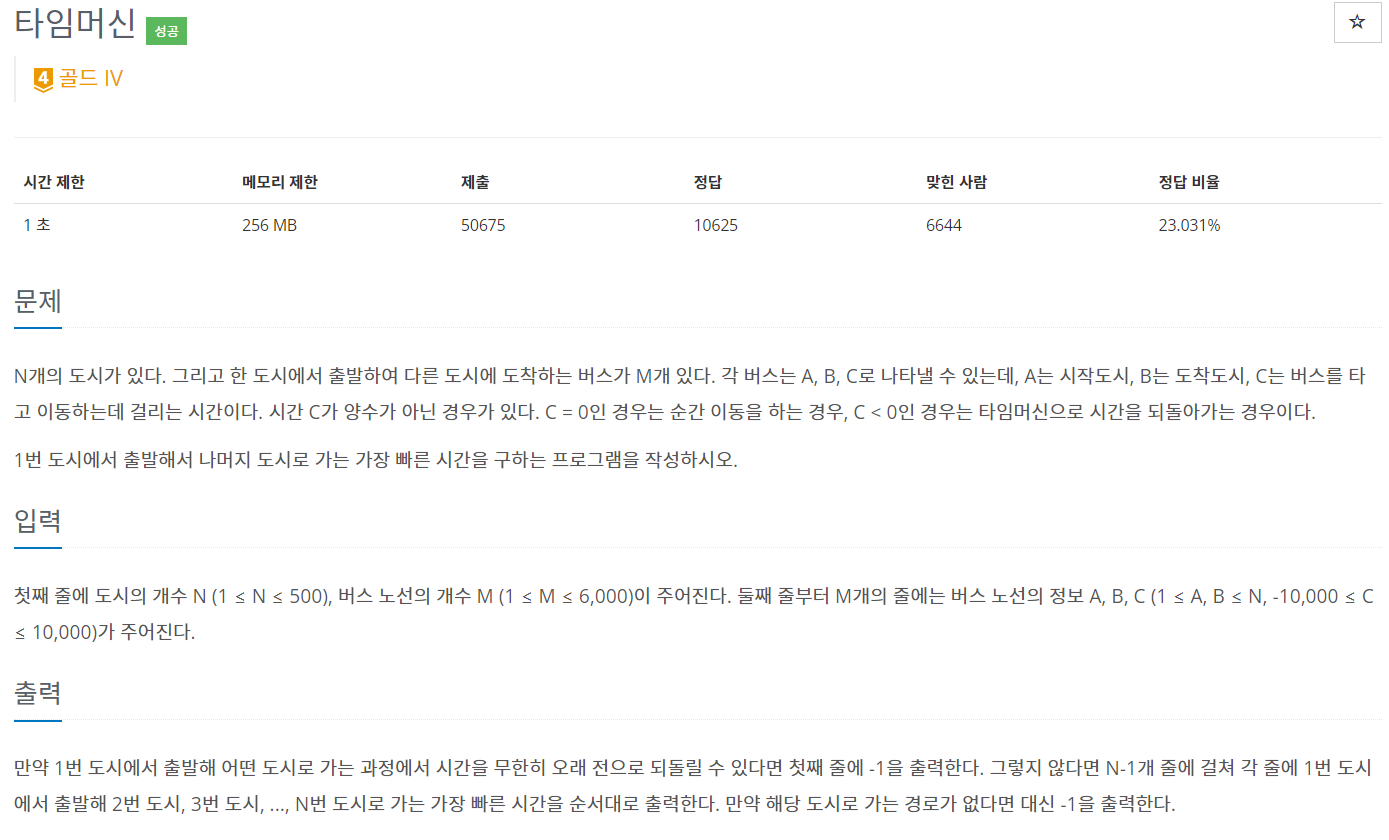
✅문제 - [백준] 타임머신 (11657번) 

---

 

✅필요 알고리즘 개념 - Bellaman-Ford Algorithm

---

🔵 Bellman-Ford Algorithm

Bellman-Ford 알고리즘은 한 node 에서 다른 모든 node 들로 가는 최단 거리를 구하는 알고리즘이다. 

 

🔵 Bellman-Ford Algorithm 와 Dijkstra Algorithm의 차이

1. Dijkstra Algorithm는 음의 가중치를 갖지 않는 상황에서 사용한다.

이때 순간순간 가중치가 가장 작은 간선을 선택하는 것이 최단거리를 보장하므로 Greedy와 Priority Que를 이용하여 구현할 수 있다.

 

2. Bellman Ford Algorithm은 음의 가중치를 갖는 상황에서 사용한다.

이때는 가중치가 가장 작은 간선을 선택하는 것이 최단 거리를 보장하지 않으므로 DP를 이용해 구현한다.

이때 음의 Cycle을 가지게 되면 음의 사이클을 돌면 계속해서 최단거리가 줄어들게 되므로 음의 Cycle의 유무를 확인한다

 

 

 

✅코드

---

import sys
from collections import deque
import heapq

INF = 10**8

# f = open("C:/Users/Hoo/Desktop/BaekJoon/test_case.txt", "r")
# instructions = f.readlines()
instructions = sys.stdin.readlines()

vertices, edge = map(int, instructions[0].rstrip().split())
graphs = []
# 1. Distance와 Predecessor 생성
distance = [INF for _ in range(vertices + 1)]
distance[1] = 0
predecessor = [-1 for _ in range(vertices + 1)]
minus_cycle = False

for instruction in instructions[1:]:
    depart, arrive, cost = map(int, instruction.rstrip().split())
    graphs.append((depart, arrive, cost))

# vertices - 1 번 동안 모든 edge들을 돌며 최단거리 갱신
# distance[u]==INF인 경우 가지 못하는 node이므로 갱신에서 제외
for i in range(vertices - 1):
    for u, v, c in graphs:
        if distance[u] == INF:
            continue
        if distance[u] + c < distance[v]:
            distance[v] = distance[u] + c
            predecessor[v] = u


# 음의 Cycle 검출
# 이 때 시작 node에서 가지 못하는 곳에서 생기는 음의 Cycle은 상관 없으므로
# distance[u] == INF인 경우. 즉, 시작 node에서 가지 못하는 경우는 제외한다.
for u, v, c in graphs:
    if distance[u] == INF:
        continue
    if distance[u] + c < distance[v]:
        minus_cycle = True

if minus_cycle:
    print(-1)
else:
    for i in distance[2:]:
        if i >= INF:
            print(-1)
        else:
            print(i)