Q1) 20000 이하의 친화수 구하기
1) 개념
- 친화수 ( 어느 한 수의 진약수를 더하면 다른 수가 되는 수, 이 때 다른 수의 진약수의 합은 원래 수가 된다. )
2) code
num_list = [0,0,1]
#뒤에 나올 반복문 range의 번호와 num_list index 번호를 맞추기 위해 0,0,을 삽입
#range가 2일 때의 값 1을 미리 넣고 range를 3부터 시작
sum = 1
#1은 모든 수의 약수이므로 약수의 합 sum의 기본 값으로 1을 설정
for i in range(3,20000):
for num in range(2,i):
if i%num ==0:
sum += num
#i를 i-1이하의 숫자로 나누고 나머지가 0인 경우 sum에 더한다.
num_list.append(sum)
#num_list[i]에 i의 약수의 합인 sum을 추가한다.
sum = 1
#sum을 초기화
#이렇게 1~20000까지의 숫자의 약수의 합을 성분으로 가지는 num_list를 만든다.
for i in range(2,20000):
if num_list[i] <=1:
continue
#sum = 1 이면 소수이므로 무시하고 다음 반복문으로 넘어간다.
else:
for j in range(i+1,20000):
#i 미만의 숫자는 그 전 반복문에서 이미 수행했으므로 i+1부터 시작
if num_list[i] == j and num_list[j] == i:
# 중요 ! num_list[i] = 자연수 i의 약수의 합
# 그러므로 i의 약수의 합 = j 이고 j의 약수의 합이 i 이면
# 두 수의 관계를 친화수라고 한다.
print(f"{i} 친화수 {j}" )
print(f"{j} 친화수 {i}" )
3) 결과
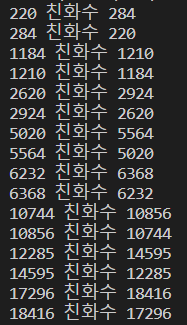
4) 문제점
친화수 문제를 풀면서 약수의 합 sum이 != 1 인 경우에만 num_list에 추가했더니 원래의 수와 num_list의 index번호가 맞지 않는 문제가 있어 어려움을 겪었다.
그래서 결국 모든 수를 list에 추가하기로 하였다.
그리고 친화수를 만족시키는 논리구조를 해결하는 부분이 어려웠다.
그리고 실행시에 많은 시간이 걸리는 것으로 보아 비효율적인 코드인 것 같고 개선이 필요해 보인다.
Q2) 20000 이하의 완전수 구하기
1) 개념
- 완전수 : 어떤 정수 n의 자기자신을 제외한 약수 (진약수)의 합이 자기 자신(n)이 되는 수를 완전수라고 한다.
2) code
perfect_num = []
#완전수를 담을 빈 list
for i in range(20000):
sum = 1
#약수의 합을 의미하는 sum
#1은 모든 수의 약수이므로 sum=1로 시작한다.
#반복문이 시작될 때마다 sum = 1로 초기화 시킨다.
for j in range(2,i-1):
if i%j ==0:
sum += j
#2~(i-1)까지의 수로 나눈 후 나머지가 0이면 sum에 더한다.
if i == sum:
perfect_num.append(sum)
#피제수 i와 i의 진약수의 합이 같으면 perfect_num에 추가한다.
print(perfect_num)
3) 결과

'Algorithm & Data Structure' 카테고리의 다른 글
| [백준] 구간성분(10840번) - 해싱 (0) | 2022.10.10 |
|---|---|
| [Today I Learned] 알고리즘 기초와 배열 (0) | 2022.09.28 |
| [백준] 그룹단어체커 (1316번) - Python (1) | 2022.09.28 |
| txt 작업 ( readlines 메소드 / 공백 제거 ) (1) | 2022.09.21 |
| for문 사용시에 list 자료형과, set 자료형의 차이 (0) | 2022.09.17 |
